mean shift算法详解
- Sunny
- 0
- Posted on
所谓mean shift,即为滑动均值聚类,是无监督学习的一种,通常用于目标检测,也可以用来做分类识别。
MS(mean shift)算法的优势在于可以使用完全无标注的数据进行分类任务。MS算法已经在sklearn中实现,可以直接调用对应的函数进行分类任务。接下来我们对这个算法的原理及主要思想和实例应用进行讲解。
算法原理
均值漂移的基本形式(shift base)
给定d维空间的n个数据点集X那么对于空间中任意点x的MS向量基本形式可以表示为:
\pmb M_h = \frac{1}{K}\sum_{x_i\in \pmb S_k}(\pmb{X}_i - \pmb{X}_0) = \frac{\sum_{x_i\in S_k}w_i(X_0)X_i}{\sum_{x_i\in S_k}w_i(X_0)}-X_0 \tag{1}这个向量被称为漂移向量,其中[katex]S_k[\katex]表示的是数据集的点到x的距离小于球半径h的数据点,第二项式子是将原有的表达式改写成权重形式,这方便后续引进核函数的概念。
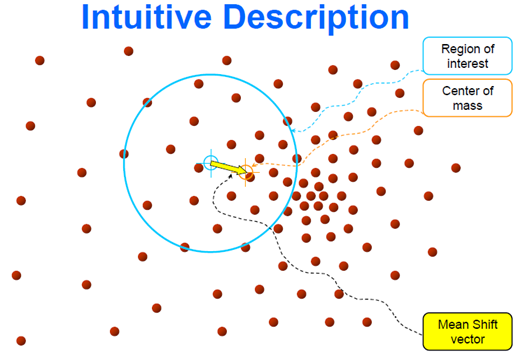
简单来说就是:
\pmb S_k = \{\pmb Y:(\pmb Y-\pmb X_i)_T(\pmb Y-\pmb X_i) < h^2\}漂移向量得出后,可以通过这个量确定下一个超球的中心点:
\pmb {X'}=\hat {f}_{h,K}(X)= \pmb {X}_0 + \pmb M_h = \frac{C_{k,d}}{nh^d}\sum_{x_i\in \pmb S_k}k\begin{pmatrix}\begin{Vmatrix}\frac{\pmb X_0-\pmb X_i}{h}\end{Vmatrix}\end{pmatrix} \tag{2}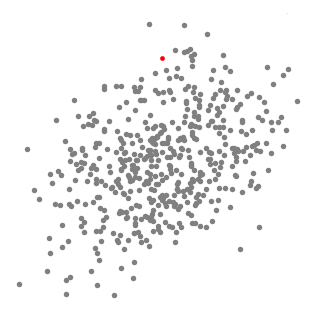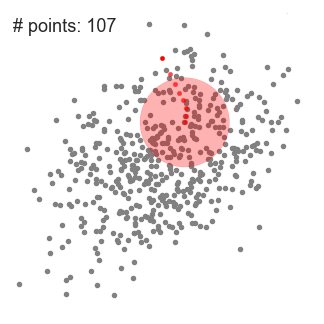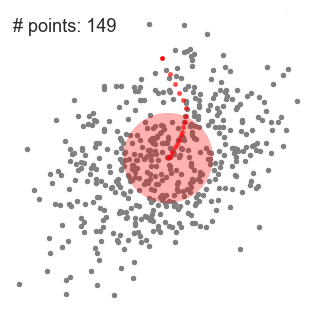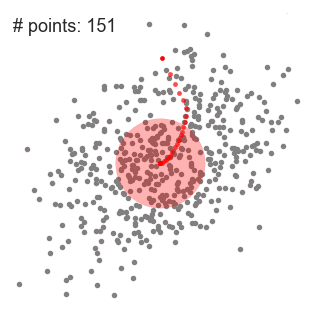
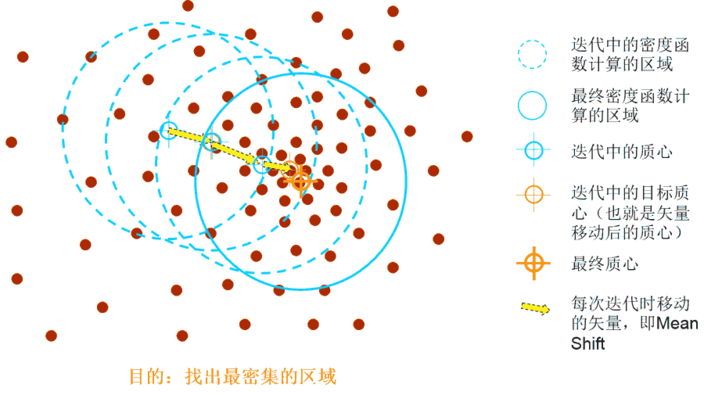
然后迭代,使得超球一直往质心方向移动。
总结来说就是,求解超球范围内的所有样本点的质心,将质心做为下一次超球的中心点,通过不断迭代计算,找到样本集中局部密度最大点。

加入高斯核函数的均值漂移
加入核函数其实就是在原有的漂移向量上引入高斯权重,使表达式变为:
\pmb M_h = \frac {\sum_{x_i\in S_k}\pmb X_ig\begin{pmatrix} \begin{Vmatrix}\frac{\pmb X_0-\pmb X_i}{h}\end{Vmatrix} \end{pmatrix}}{\sum_{x_i\in S_k}g\begin{pmatrix} \begin{Vmatrix}\frac{\pmb X_0-\pmb X_i}{h}\end{Vmatrix} \end{pmatrix}}-\pmb X_0则(2)式引入高斯核函数后求导可得:
\nabla\hat {f}_{h,K}(\pmb X_0) = \hat {f}_{h,K}(X) \frac{2C_{k,d}}{h^2C_{k,d}}\pmb m_{h,K}(\pmb X_0)我们知道,要使得球心移动到密度最大的点,漂移向量单步步长应为0,且其全导为0。
因此要使得[katex]\nabla\hat {f}_{h,K}(\pmb X0)=0[\katex],当且仅当[katex]\pmb m{h,K}(\pmb X_0)=0[\katex]时,可以取得新的球心坐标
\pmb X' = \frac {\sum_{x_i\in S_k}\pmb X_ig\begin{pmatrix} \begin{Vmatrix}\frac{\pmb X_0-\pmb X_i}{h}\end{Vmatrix} \end{pmatrix}}{\sum_{x_i\in S_k}g\begin{pmatrix} \begin{Vmatrix}\frac{\pmb X_0-\pmb X_i}{h}\end{Vmatrix} \end{pmatrix}}